Surface Constraint

Following on from last week, I've been looking at how to build something similar to the geometry constraint in Maya.

It's certainly a tricky one. I've just found out about tangents and binormals which I'm still struggling to grasp but they are useful for building a somewhat stable surface based matrix..i think.

I'd like to do a bit of a write up on it soon, there's so many things I'm not too sure about. 

For one thing, using MFnMesh.getClosestPointAndNormal() won't return a normal in world space if I'm getting the mesh data using inputValue.asMeshTransformed(). Is this a bug? Maybe I'm using it wrong.

Here's a quick demo. 

Vertex Constraint aka Rivet

Just a quick update this week. I learnt some cool stuff to do with building matrixes...or matrices. Yea..matrices.

As far as I can tell thus far in my investigations, you need the following basic ingredients to start with:

1) A unit vector
2) The normalized cross product of 1) and any vector that isn't a scalar of 1) *
3) The cross product of the vector from 1) and 2). Again, needs to be normalized
4) A point

I picked up a good maths intro series from Chad Vernon to which he alluded how to build something that resembles the classic rivet constraint. It was an interesting challenge to take on as I only had some clues to go by, not a step by step guide. I'm glad I stuck with it and got something working in the end.

I've tested it on a skinned mesh with blendshapes and its doing the job so far. Yea..I can't believe it either.


Thanks http://www.hippydrome.com/ for the free model.





* I wonder what happens when you take the cross product of a and -a...

Line Plane Intersection

I went with line plane intersection this time around, for a couple of reasons.

First off, there's some excellent info on it already, This one really solidified it for me because it broke the process down step by step.

Having said that, these sorts of topics can be difficult to look at on paper sometimes..I mean, how does one go about visualizing the equation for a plane?

Anyway, on to it. I built this node in C++ using one of the examples in the devkit as a template. Surprisingly, there isn't too much manual work if it's a relatively simple compute and starting from a template makes things much easier. I think I spent the majority of the time learning the syntax for different input attributes.

As there is already so much good info out there for this topic, I'll just go over the first couple of steps of how I got the normal of the plane, without using any of the convenience methods in MFnMesh, MItGeometry etc.

---------------------------------------------

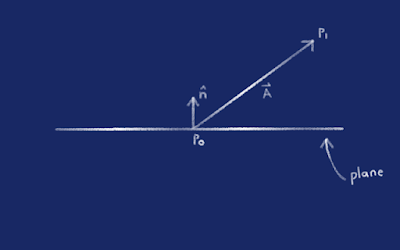
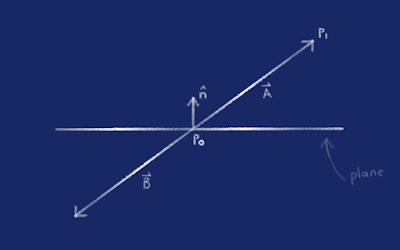
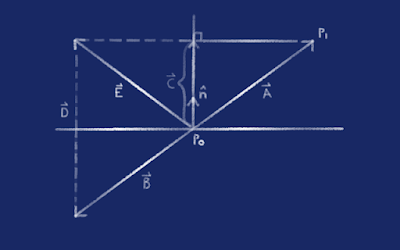
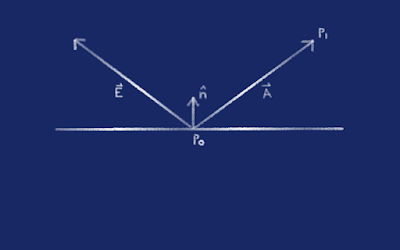
First off, we're looking for pX. The point of intersection with the plane if we were to extend the vector from p0 to p1. Think of it kinda like shining a torch onto the floor, and you're aiming the torch 5 metres in front of you. You can roughly gauge where the light will hit, but where exactly is it going to hit? Using this example, p0 is the butt* of the torch and p1 is the light cone or front of the torch.



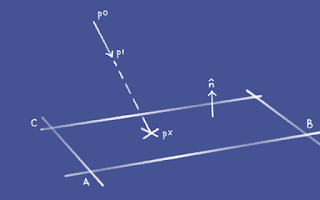
To start off with, we need to get the normal of the plane, a vector perpendicular to the plane. It's labelled n in the picture above.

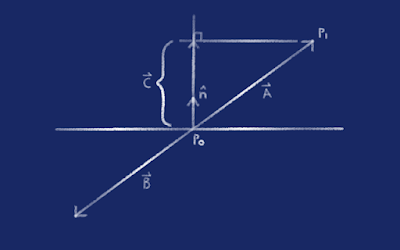
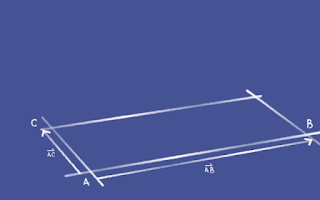
Imagine the plane as a polygon that covers a floor, and the points A, B & C as the corner points. The floor might have a fourth point (corner) or more, but we only need three points to define a plane.

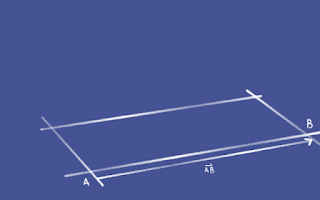
Get the vector from A to B.

AB = B - A



Now get the vector from A to C.

AC = C - A



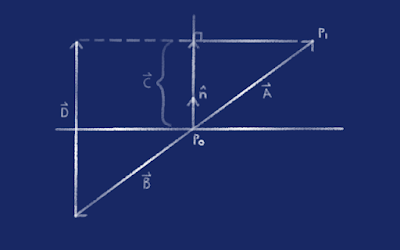
Take the cross product of AB and AC. This will give you a vector perpendicular to both AB and AC.
It matters which way round you do this as there are actually two vectors perpendicular to the plane (think towards the ceiling and down through the floor..).

AD = AC x AB



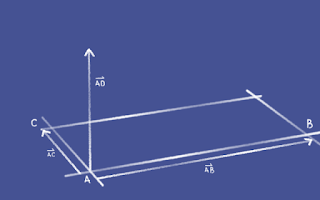
Now we have our vector AD, it's just a case of turning it into a unit vector, represented as n in the first image.

Check out the tutorials I've linked to at the start to go from here.


Here's a quick demo of the C++ node in action.





Use case example: Finding a position for a pole vector

I re-built it in Python to take in the three points we need to define a plane. If I connect up the three joints of an arm or leg we can find a position for a pole vector that won't offset the joints when applied.
I'll admit, it's probably not the best way to go about building a pole vector but still, I think it's good insight to how the pole vector stuff works.




Downloads:
Plugin (Python)




* heh

Reflecting a Vector

As you can probably guess, I went with learning about reflecting a vector as it hits a point on a plane.
I like to visualize it as shining a laser pen onto a mirror. cool eh?

There's tons of examples around so I worked my way through them and tried building something similar using expressions or vanilla Maya nodes. When I got something working I built a custom node.
The blue locator represents the source vector A, the plane has the normal n and the point P. The resulting reflected vector B, is the red locator.

 

There's a few calculations we can skip if the plane is static, but it'd be kinda cool to move the plane around and see what the reflection would be. Here's how I went about it:

Get the vector A.

A = P1 - P0

--------

Reverse the Vector A by multiplying it by -1 and add it to P0.

B = ( -1 * A ) + P0

--------

Project A onto the normal n, using the dot product. There's plenty of resources online if you're not sure what the dot product does.

C = ( A • n ) * n

--------

Multiply C by 2 and add to the vector B.

D = ( 2 * C ) + B

--------

We can find the vector E by subtracting the end point of vector D from P0.


--------

Final reflected vector.





Here's a quick demo. :D




Downloads:
Scene file setup with standard math nodes.
Plugin (Python)

If you check out the python script, you'll notice I'm not using the plane normal. I could have probably used a mesh function set to get a face or vertex normal but I cheated a bit and used the Y basis vector from the worldMatrix of the plane transform.

What happens if the plane has multiple faces, which normal do we choose?

Obligatory first post!

At the start of the year I set myself the insurmountable task of getting to grips with the Maya API. I thought a blog would be a great way to record my progress* and share what I learn*.

Anyway, I'll give it a go. Along the way I'll be attempting to brush up on my maths by way of vectors and all that good stuff. 

*living hell
*die from